Feb 18 2021
Off

AWS Feed
Solving numerical optimization problems like scheduling, routing, and allocation with Amazon SageMaker Processing

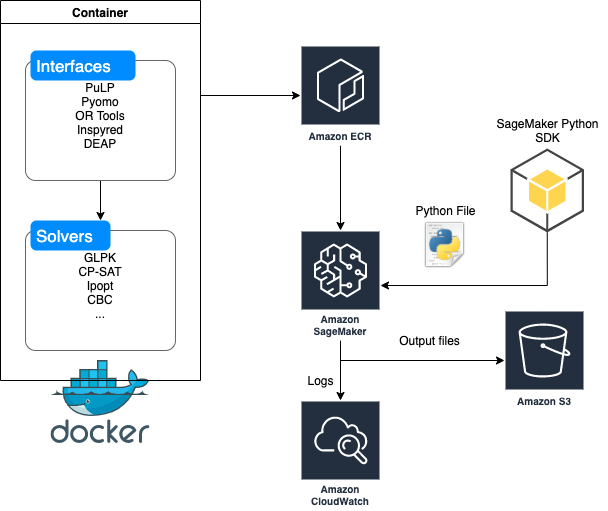
In this post, we discuss solving numerical optimization problems using the very flexible Amazon SageMaker Processing API. Optimization is the process of finding the minimum (or maximum) of a function that depends on some inputs, called design variables. This pattern is relevant to solving business-critical problems such as scheduling, routing, allocation, shape optimization, trajectory optimization, and others. Several commercial and open-source solvers are available for solving such problems. We demonstrate this solution with three popular Python libraries and solvers that are free to use, and provide a sample notebook that shows how to solve these optimization problems using SageMaker Processing.

Solution overview

SageMaker Processing lets data scientists and ML engineers easily run preprocessing, postprocessing, and model evaluation workloads on SageMaker. This SDK uses the built-in container for scikit-learn and Spark. You can also use your own Docker images without having to conform to any Docker image specification. This gives you maximum flexibility in running any code you want, whether on SageMaker Processing, on AWS container services like Amazon Elastic Container Service (Amazon ECS) and Amazon Elastic Kubernetes Service (Amazon EKS), or even on premises; which is what we do in this post. First, we build and push a Docker image that includes several popular optimization packages and solvers, and then we use this Docker image to solve three example problems:

  • Minimize the cost of shipping goods through a distribution network
  • Scheduling shifts of a set of nurses in a hospital
  • Find a trajectory for landing the Apollo 11 Lunar Module with the least amount of fuel

We solve each use case using a different interface that connects to a different solver. We complete the following high-level steps (as in the provided example notebook) for each problem:

  1. Build a Docker container that contains useful Python interfaces (such as Pyomo and PuLP) to optimization solvers (such as GLPK and CBC)
  2. Build and push the image to a repository in Amazon Elastic Container Registry (Amazon ECR).
  3. Use the SageMaker Python SDK (from a notebook or elsewhere with the right permissions) to point to the Docker image in Amazon ECR and send in a Python file with the actual optimization problem.
  4. Monitor the logs in a notebook or Amazon CloudWatch Logs and obtain and outputs you need in a dedicated output folder that you specify in Amazon Simple Storage Service (Amazon S3).

Schematically, this process looks like the following diagram.

Schematically, this process looks like the following diagram.

Let’s get started!

Building and pushing a Docker container

Start with the following Dockerfile:

FROM continuumio/anaconda3 RUN pip install boto3 pandas scikit-learn pulp pyomo inspyred ortools scipy deap RUN conda install -c conda-forge ipopt coincbc glpk ENV PYTHONUNBUFFERED=TRUE ENTRYPOINT ["python"]

In this code, we install Python interfaces to solvers such as PuLP, Pyomo, Inspyred, OR-Tools, Scipy, and DEAP. For more information about these solvers, see the References section at the end of this post.

We then use the following commands from the notebook to build and push this container to Amazon ECR:

import boto3 account_id = boto3.client('sts').get_caller_identity().get('Account')
ecr_repository = 'sagemaker-opt-container'
tag = ':latest'
processing_repository_uri = '{}.dkr.ecr.{}.amazonaws.com/{}'.format(account_id, region, ecr_repository + tag) # Create ECR repository and push docker image
!docker build -t $ecr_repository docker
!$(aws ecr get-login --region $region --registry-ids $account_id --no-include-email)
!aws ecr create-repository --repository-name $ecr_repository
!docker tag {ecr_repository + tag} $processing_repository_uri
!docker push $processing_repository_uri

Sample output for this command looks like the following code:

Sending build context to Docker daemon 2.048kB
Step 1/5 : FROM continuumio/anaconda3 ---> 5fbf7bac70a0
Step 2/5 : RUN pip install boto3 pandas scikit-learn pulp pyomo inspyred ortools scipy deap ---> Using cache ---> 98864164a472
Step 3/5 : RUN conda install -c conda-forge ipopt coincbc glpk ---> Using cache ---> 1fde58988350
Step 4/5 : ENV PYTHONUNBUFFERED=TRUE ---> Using cache ---> 06cc27c84a9a
Step 5/5 : ENTRYPOINT ["python"] ---> Using cache ---> 0ae65a2ad5b9
Successfully built <code>
Successfully tagged sagemaker-opt-container:latest
WARNING! Using --password via the CLI is insecure. Use --password-stdin.
WARNING! Your password will be stored unencrypted in /home/ec2-user/.docker/config.json.
Configure a credential helper to remove this warning. See
https://docs.docker.com/engine/reference/commandline/login/#credentials-store Login Succeeded An error occurred (RepositoryAlreadyExistsException) when calling the CreateRepository operation: The repository with name 'sagemaker-opt-container' already exists in the registry with id '<account numnber>'
The push refers to repository [<account number>.dkr.ecr.<region>.amazonaws.com/sagemaker-opt-container] 8611989d: Preparing d960633d: Preparing db96c31c: Preparing ea6160d7: Preparing 4bce66cd: Layer already exists latest: digest: sha256:<hash> size: 1379

Using the SageMaker Python SDK to start a job

Typically, we first initialize a SageMaker Processing ScriptProcessor as follows:

from sagemaker.processing import ScriptProcessor script_processor = ScriptProcessor(command=['python'], image_uri=processing_repository_uri, role=role, instance_count=1, instance_type='ml.m5.xlarge')

Then we write a file (for this post, we always use a file called preprocessing.py) and run a processing job on SageMaker as follows:

from sagemaker.processing import ProcessingInput, ProcessingOutput script_processor.run(code='preprocessing.py', outputs=[ProcessingOutput(output_name='data', source='/opt/ml/processing/data')]) script_processor_job_description = script_processor.jobs[-1].describe()
print(script_processor_job_description)

Use case 1: Minimizing the cost of shipping goods through a distribution network

In this use case, American Steel, an Ohio-based steel manufacturing company, produces steel at its two steel mills located at Youngstown and Pittsburgh. The company distributes finished steel to its retail customers through the distribution network of regional and field warehouses.

The network represents shipment of finished steel from American Steel—two steel mills located at Youngstown (node 1) and Pittsburgh (node 2) to their field warehouses at Albany, Houston, Tempe, and Gary (nodes 6, 7, 8, and 9) through three regional warehouses located at Cincinnati, Kansas City, and Chicago (nodes 3, 4, and 5). Also, some field warehouses can be directly supplied from the steel mills.

The following table presents the minimum and maximum flow amounts of steel that may be shipped between different cities, along with the cost per 1,000 tons per month of shipping the steel. For example, the shipment from Youngstown to Kansas City is contracted out to a railroad company with a minimal shipping clause of 1,000 tons per month. However, the railroad can’t ship more than 5,000 tons per month due the shortage of rail cars.

From node To node Cost Minimum Maximum
Youngstown Albany 500 – 1000
Youngstown Cincinnati 350 – 3000
Youngstown Kansas City 450 1000 5000
Youngstown Chicago 375 – 5000
Pittsburgh Cincinnati 350 – 2000
Pittsburgh Kansas City 450 2000 3000
Pittsburgh Chicago 400 – 4000
Pittsburgh Gary 450 – 2000
Cincinnati Albany 350 1000 5000
Cincinnati Houston 550 – 6000
Kansas City Houston 375 – 4000
Kansas City Tempe 650 – 4000
Chicago Tempe 600 – 2000
Chicago Gary 120 – 4000

The objective of transshipment problems in general and The American Steel Problem in particular is to minimize the cost of shipping goods through the network.

All the nodes have supply and demand, demand = 0 for supply nodes, supply = 0 for demand nodes, and supply = demand = 0 for transshipment nodes. The only constraints in the transshipment problem are flow conservation constraints. These constraints simply state that the flow of goods into a node must be greater than or equal to the flow of goods out of a node.

This problem can be formulated as follows:

%%writefile preprocessing.py import argparse
import os
import warnings """
The American Steel Problem for the PuLP Modeller Authors: Antony Phillips, Dr Stuart Mitchell 2007
""" # Import PuLP modeller functions
from pulp import * # List of all the nodes
Nodes = ["Youngstown", "Pittsburgh", "Cincinatti", "Kansas City", "Chicago", "Albany", "Houston", "Tempe", "Gary"] nodeData = {# NODE Supply Demand "Youngstown": [10000,0], "Pittsburgh": [15000,0], "Cincinatti": [0,0], "Kansas City": [0,0], "Chicago": [0,0], "Albany": [0,3000], "Houston": [0,7000], "Tempe": [0,4000], "Gary": [0,6000]} # List of all the arcs
Arcs = [("Youngstown","Albany"), ("Youngstown","Cincinatti"), ("Youngstown","Kansas City"), ("Youngstown","Chicago"), ("Pittsburgh","Cincinatti"), ("Pittsburgh","Kansas City"), ("Pittsburgh","Chicago"), ("Pittsburgh","Gary"), ("Cincinatti","Albany"), ("Cincinatti","Houston"), ("Kansas City","Houston"), ("Kansas City","Tempe"), ("Chicago","Tempe"), ("Chicago","Gary")] arcData = { # ARC Cost Min Max ("Youngstown","Albany"): [0.5,0,1000], ("Youngstown","Cincinatti"): [0.35,0,3000], ("Youngstown","Kansas City"): [0.45,1000,5000], ("Youngstown","Chicago"): [0.375,0,5000], ("Pittsburgh","Cincinatti"): [0.35,0,2000], ("Pittsburgh","Kansas City"): [0.45,2000,3000], ("Pittsburgh","Chicago"): [0.4,0,4000], ("Pittsburgh","Gary"): [0.45,0,2000], ("Cincinatti","Albany"): [0.35,1000,5000], ("Cincinatti","Houston"): [0.55,0,6000], ("Kansas City","Houston"): [0.375,0,4000], ("Kansas City","Tempe"): [0.65,0,4000], ("Chicago","Tempe"): [0.6,0,2000], ("Chicago","Gary"): [0.12,0,4000]} # Splits the dictionaries to be more understandable
(supply, demand) = splitDict(nodeData)
(costs, mins, maxs) = splitDict(arcData) # Creates the boundless Variables as Integers
vars = LpVariable.dicts("Route",Arcs,None,None,LpInteger) # Creates the upper and lower bounds on the variables
for a in Arcs: vars[a].bounds(mins[a], maxs[a]) # Creates the 'prob' variable to contain the problem data prob = LpProblem("American Steel Problem",LpMinimize) # Creates the objective function
prob += lpSum([vars[a]* costs[a] for a in Arcs]), "Total Cost of Transport" # Creates all problem constraints - this ensures the amount going into each node is at least equal to the amount leaving
for n in Nodes: prob += (supply[n]+ lpSum([vars[(i,j)] for (i,j) in Arcs if j == n]) >= demand[n]+ lpSum([vars[(i,j)] for (i,j) in Arcs if i == n])), "Steel Flow Conservation in Node %s"%n # The problem data is written to an .lp file
prob.writeLP('/opt/ml/processing/data/' + 'AmericanSteelProblem.lp') # The problem is solved using PuLP's choice of Solver
prob.solve() # The status of the solution is printed to the screen
print("Status:", LpStatus[prob.status]) # Each of the variables is printed with it's resolved optimum value
for v in prob.variables(): print(v.name, "=", v.varValue) # The optimised objective function value is printed to the screen print("Total Cost of Transportation = ", value(prob.objective))

We solve this problem using the PuLP interface and its default solver GLPK using script_processor.run. Logs from this optimization job provide these solutions:

Status: Optimal
Route_('Chicago',_'Gary') = 4000.0
Route_('Chicago',_'Tempe') = 2000.0
Route_('Cincinatti',_'Albany') = 2000.0
Route_('Cincinatti',_'Houston') = 3000.0
Route_('Kansas_City',_'Houston') = 4000.0
Route_('Kansas_City',_'Tempe') = 2000.0
Route_('Pittsburgh',_'Chicago') = 3000.0
Route_('Pittsburgh',_'Cincinatti') = 2000.0
Route_('Pittsburgh',_'Gary') = 2000.0
Route_('Pittsburgh',_'Kansas_City') = 3000.0
Route_('Youngstown',_'Albany') = 1000.0
Route_('Youngstown',_'Chicago') = 3000.0
Route_('Youngstown',_'Cincinatti') = 3000.0
Route_('Youngstown',_'Kansas_City') = 3000.0
Total Cost of Transportation = 15005.0

Use case 2: Scheduling shifts of a set of nurses in a hospital

In the next example, a hospital supervisor must create a schedule for four nurses over a 3-day period, subject to the following conditions:

  • Each day is divided into three 8-hour shifts
  • Every day, each shift is assigned to a single nurse, and no nurse works more than one shift
  • Each nurse is assigned to at least two shifts during the 3-day period

For more information about this scheduling use case, see Employee Scheduling.

This problem can be formulated as follows:

%%writefile preprocessing.py from __future__ import print_function
from ortools.sat.python import cp_model class NursesPartialSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, shifts, num_nurses, num_days, num_shifts, sols): cp_model.CpSolverSolutionCallback.__init__(self) self._shifts = shifts self._num_nurses = num_nurses self._num_days = num_days self._num_shifts = num_shifts self._solutions = set(sols) self._solution_count = 0 def on_solution_callback(self): if self._solution_count in self._solutions: print('Solution %i' % self._solution_count) for d in range(self._num_days): print('Day %i' % d) for n in range(self._num_nurses): is_working = False for s in range(self._num_shifts): if self.Value(self._shifts[(n, d, s)]): is_working = True print(' Nurse %i works shift %i' % (n, s)) if not is_working: print(' Nurse {} does not work'.format(n)) print() self._solution_count += 1 def solution_count(self): return self._solution_count def main(): # Data. num_nurses = 4 num_shifts = 3 num_days = 3 all_nurses = range(num_nurses) all_shifts = range(num_shifts) all_days = range(num_days) # Creates the model. model = cp_model.CpModel() # Creates shift variables. # shifts[(n, d, s)]: nurse 'n' works shift 's' on day 'd'. shifts = {} for n in all_nurses: for d in all_days: for s in all_shifts: shifts[(n, d, s)] = model.NewBoolVar('shift_n%id%is%i' % (n, d, s)) # Each shift is assigned to exactly one nurse in the schedule period. for d in all_days: for s in all_shifts: model.Add(sum(shifts[(n, d, s)] for n in all_nurses) == 1) # Each nurse works at most one shift per day. for n in all_nurses: for d in all_days: model.Add(sum(shifts[(n, d, s)] for s in all_shifts) <= 1) # min_shifts_per_nurse is the largest integer such that every nurse # can be assigned at least that many shifts. If the number of nurses doesn't # divide the total number of shifts over the schedule period, # some nurses have to work one more shift, for a total of # min_shifts_per_nurse + 1. min_shifts_per_nurse = (num_shifts * num_days) // num_nurses max_shifts_per_nurse = min_shifts_per_nurse + 1 for n in all_nurses: num_shifts_worked = sum( shifts[(n, d, s)] for d in all_days for s in all_shifts) model.Add(min_shifts_per_nurse <= num_shifts_worked) model.Add(num_shifts_worked <= max_shifts_per_nurse) # Creates the solver and solve. solver = cp_model.CpSolver() solver.parameters.linearization_level = 0 # Display the first five solutions. a_few_solutions = range(5) solution_printer = NursesPartialSolutionPrinter(shifts, num_nurses, num_days, num_shifts, a_few_solutions) solver.SearchForAllSolutions(model, solution_printer) # Statistics. print() print('Statistics') print(' - conflicts : %i' % solver.NumConflicts()) print(' - branches : %i' % solver.NumBranches()) print(' - wall time : %f s' % solver.WallTime()) print(' - solutions found : %i' % solution_printer.solution_count()) if __name__ == '__main__': main()

We solve this problem using the OR-Tools interface and its CP-SAT solver with script_processor.run. Logs from this optimization job provide these solutions:

Solution 0
Day 0 Nurse 0 does not work Nurse 1 works shift 0 Nurse 2 works shift 1 Nurse 3 works shift 2
Day 1 Nurse 0 works shift 2 Nurse 1 does not work Nurse 2 works shift 1 Nurse 3 works shift 0
Day 2 Nurse 0 works shift 2 Nurse 1 works shift 1 Nurse 2 works shift 0 Nurse 3 does not work Solution 1
Day 0 Nurse 0 works shift 0 Nurse 1 does not work Nurse 2 works shift 1 Nurse 3 works shift 2
Day 1 Nurse 0 does not work Nurse 1 works shift 2 Nurse 2 works shift 1 Nurse 3 works shift 0
Day 2 Nurse 0 works shift 2 Nurse 1 works shift 1 Nurse 2 works shift 0 Nurse 3 does not work Solution 2
Day 0 Nurse 0 works shift 0 Nurse 1 does not work Nurse 2 works shift 1 Nurse 3 works shift 2
Day 1 Nurse 0 works shift 1 Nurse 1 works shift 2 Nurse 2 does not work Nurse 3 works shift 0
Day 2 Nurse 0 works shift 2 Nurse 1 works shift 1 Nurse 2 works shift 0 Nurse 3 does not work Solution 3
Day 0 Nurse 0 works shift 0 Nurse 1 does not work Nurse 2 works shift 1 Nurse 3 works shift 2
Day 1 Nurse 0 works shift 2 Nurse 1 works shift 1 Nurse 2 does not work Nurse 3 works shift 0
Day 2 Nurse 0 works shift 2 Nurse 1 works shift 1 Nurse 2 works shift 0 Nurse 3 does not work Solution 4
Day 0 Nurse 0 does not work Nurse 1 works shift 0 Nurse 2 works shift 1 Nurse 3 works shift 2
Day 1 Nurse 0 works shift 2 Nurse 1 works shift 1 Nurse 2 does not work Nurse 3 works shift 0
Day 2 Nurse 0 works shift 2 Nurse 1 works shift 1 Nurse 2 works shift 0 Nurse 3 does not work Statistics - conflicts : 37 - branches : 41231 - wall time : 0.367511 s - solutions found : 5184

Use case 3: Finding a trajectory for landing the Apollo 11 Lunar Module with the least amount of fuel

This example uses Pyomo and a simple model of a rocket to compute a control policy for a soft landing. The parameters used correspond to the descent of the Apollo 11 Lunar Module to the moon on July 20, 1969. For a rocket with a mass 𝑚 in vertical flight at altitude ℎ, a momentum balance yields the following model:

a momentum balance yields the following model:

 

In this model, 𝑢 is the mass flow of propellant and 𝑣𝑒 is the velocity of the exhaust relative to the rocket. In this first attempt at modeling and control, we neglect the change in rocket mass due to fuel burn.

Fuel consumption can be calculated as the following:

Fuel consumption can be calculated as the following:

We want to find a trajectory that minimizes fuel consumption:

We want to find a trajectory that minimizes fuel consumption:

This problem can be formulated as follows:

%%writefile preprocessing.py import numpy as np from pyomo.environ import *
from pyomo.dae import * #Define constants ...
# lunar module
m_ascent_dry = 2445.0 # kg mass of ascent stage without fuel
m_ascent_fuel = 2376.0 # kg mass of ascent stage fuel
m_descent_dry = 2034.0 # kg mass of descent stage without fuel
m_descent_fuel = 8248.0 # kg mass of descent stage fuel m_fuel = m_descent_fuel
m_dry = m_ascent_dry + m_ascent_fuel + m_descent_dry
m_total = m_dry + m_fuel # descent engine characteristics
v_exhaust = 3050.0 # m/s
u_max = 45050.0/v_exhaust # 45050 newtons / exhaust velocity # landing mission specifications
h_initial = 100000.0 # meters
v_initial = 1520 # orbital velocity m/s
g = 1.62 # m/s**2 m = ConcreteModel()
m.t = ContinuousSet(bounds=(0, 1))
m.h = Var(m.t)
m.u = Var(m.t, bounds=(0, u_max))
m.T = Var(domain=NonNegativeReals) m.v = DerivativeVar(m.h, wrt=m.t)
m.a = DerivativeVar(m.v, wrt=m.t) m.fuel = Integral(m.t, wrt=m.t, rule = lambda m, t: m.u[t]*m.T)
m.obj = Objective(expr=m.fuel, sense=minimize) m.ode1 = Constraint(m.t, rule = lambda m, t: m_total*m.a[t]/m.T**2 == -m_total*g + v_exhaust*m.u[t]) m.h[0].fix(h_initial)
m.v[0].fix(-v_initial) m.h[1].fix(0) # land on surface
m.v[1].fix(0) # soft landing def solve(m): TransformationFactory('dae.finite_difference').apply_to(m, nfe=50, scheme='FORWARD') SolverFactory('ipopt').solve(m, tee=True) solve(m)

We use the Pyomo interface and the nonlinear optimization solver Ipopt to solve this continuous-time, trajectory optimization problem. Logs from ScriptProcessor.run provide the following solution:

Ipopt 3.12.13: ******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization. Ipopt is released as open source code under the Eclipse Public License (EPL). For more information visit http://projects.coin-or.org/Ipopt
****************************************************************************** This is Ipopt version 3.12.13, running with linear solver mumps.
NOTE: Other linear solvers might be more efficient (see Ipopt documentation). Number of nonzeros in equality constraint Jacobian...: 448
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 154 Error in an AMPL evaluation. Run with "halt_on_ampl_error yes" to see details.
Error evaluating Jacobian of equality constraints at user provided starting point. No scaling factors for equality constraints computed!
Total number of variables............................: 201 variables with only lower bounds: 1 variables with lower and upper bounds: 51 variables with only upper bounds: 0
Total number of equality constraints.................: 151
Total number of inequality constraints...............: 0 inequality constraints with only lower bounds: 0 inequality constraints with lower and upper bounds: 0 inequality constraints with only upper bounds: 0 iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls 0 9.9999800e-05 5.00e+06 9.90e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0 1r 9.9999800e-05 5.00e+06 9.99e+02 6.7 0.00e+00 - 0.00e+00 4.29e-14R 4 2r 2.1397987e+02 5.00e+06 4.78e+08 6.7 2.14e+05 - 1.00e+00 6.83e-05f 1 3r 2.1342176e+02 5.00e+06 1.36e+08 3.2 4.37e+04 - 7.16e-01 6.16e-01f 1 4r 1.7048263e+02 4.99e+06 4.67e+07 3.2 1.60e+04 - 9.85e-01 4.16e-01f 1 5r 1.5143799e+02 4.99e+06 2.50e+07 3.2 3.57e+03 - 5.88e-01 7.62e-01f 1 6r 1.3041897e+02 4.99e+06 2.08e+07 3.2 1.89e+03 - 2.75e-01 8.14e-01f 1 7r 1.1452223e+02 4.99e+06 3.17e+04 3.2 1.97e+03 - 9.78e-01 8.18e-01f 1 8r 1.1168709e+02 4.99e+06 2.72e+05 3.2 3.36e-01 4.0 9.78e-01 1.00e+00f 1 9r 1.0774716e+02 4.99e+06 1.66e+05 3.2 4.28e+03 - 9.36e-01 9.70e-02f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls 10r 8.7784873e+01 5.00e+06 5.08e+04 3.2 3.69e+03 - 8.74e-01 7.24e-01f 1 11r 7.9008215e+01 5.00e+06 1.88e+04 2.5 1.09e+03 - 1.22e-01 8.35e-01h 1 12r 1.1960245e+02 5.00e+06 4.34e+03 2.5 1.81e+03 - 6.76e-01 1.00e+00f 1 13r 1.2344166e+02 5.00e+06 1.35e+03 1.8 1.66e+02 - 8.23e-01 1.00e+00f 1 14r 2.0065756e+02 4.99e+06 6.85e+02 1.1 4.28e+03 - 4.26e-01 1.00e+00f 1 15r 3.0115879e+02 4.99e+06 4.78e+01 1.1 9.69e+03 - 7.64e-01 1.00e+00f 1 16r 3.0355974e+02 4.99e+06 5.30e+00 1.1 4.92e+00 - 1.00e+00 1.00e+00f 1 17r 3.0555655e+02 4.99e+06 6.83e+02 0.4 7.49e+00 - 1.00e+00 1.00e+00f 1 18r 4.4494526e+02 4.97e+06 2.28e+01 0.4 2.17e+04 - 8.05e-01 1.00e+00f 1 19r 3.9588385e+02 4.97e+06 3.77e+00 0.4 4.73e+00 - 1.00e+00 1.00e+00f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls 20r 4.0158949e+02 4.97e+06 7.79e-02 0.4 5.70e-01 - 1.00e+00 1.00e+00h 1 21r 4.0076180e+02 4.97e+06 9.88e+02 -1.0 1.80e+00 - 1.00e+00 1.00e+00f 1 22r 5.4964501e+02 4.95e+06 7.59e+02 -1.0 1.57e+05 - 2.48e-01 2.32e-01f 1 23r 5.5056601e+02 4.95e+06 7.57e+02 -1.0 1.21e+05 - 1.00e+00 3.02e-03f 1 24r 5.5057553e+02 4.95e+06 7.57e+02 -1.0 1.09e+05 - 8.13e-01 3.34e-05f 1 25r 5.5898777e+02 4.95e+06 7.00e+02 -1.0 3.82e+04 - 1.00e+00 7.48e-02f 1 26r 6.0274077e+02 4.96e+06 3.93e+02 -1.0 3.53e+04 - 1.00e+00 4.39e-01f 1 27r 6.0301192e+02 4.96e+06 3.90e+02 -1.0 1.98e+04 - 1.00e+00 7.83e-03f 1 28r 6.0301418e+02 4.96e+06 3.89e+02 -1.0 1.61e+04 - 1.00e+00 9.62e-05f 1 29r 5.9834909e+02 4.96e+06 3.71e+02 -1.0 3.63e+03 - 1.00e+00 1.85e-01f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls 30r 5.7601446e+02 4.95e+06 1.67e+00 -1.0 2.96e+03 - 1.00e+00 1.00e+00f 1 31r 5.6977301e+02 4.95e+06 6.41e-02 -1.0 1.22e+00 - 1.00e+00 1.00e+00h 1 32r 5.7024128e+02 4.95e+06 9.05e-05 -1.0 4.89e-02 - 1.00e+00 1.00e+00h 1 33r 5.6989454e+02 4.95e+06 6.84e+02 -2.5 9.30e-02 - 1.00e+00 1.00e+00f 1 34r 5.7613459e+02 4.94e+06 5.38e+02 -2.5 5.65e+04 - 4.67e-01 2.13e-01f 1 35r 5.7617358e+02 4.94e+06 5.37e+02 -2.5 4.45e+04 - 1.00e+00 9.52e-04f 1 36r 6.6264177e+02 4.90e+06 3.78e+01 -2.5 4.45e+04 - 6.62e-01 9.30e-01f 1 37r 7.5101828e+02 4.90e+06 7.59e+01 -2.5 3.12e+03 - 1.25e-02 1.00e+00f 1 38r 7.5705424e+02 4.90e+06 8.60e-02 -2.5 7.04e-01 - 1.00e+00 1.00e+00h 1 39r 7.5713736e+02 4.90e+06 2.85e-05 -2.5 9.02e-03 - 1.00e+00 1.00e+00h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls 40r 7.5713093e+02 4.90e+06 4.90e+02 -5.7 6.76e-03 - 1.00e+00 9.99e-01f 1 41r 1.0909809e+03 4.78e+06 4.67e+02 -5.7 2.54e+06 - 6.15e-02 4.62e-02f 1 42r 1.0909867e+03 4.78e+06 4.67e+02 -5.7 2.42e+06 - 1.00e+00 9.55e-07f 1 43r 1.5672936e+03 4.59e+06 8.15e+03 -5.7 2.42e+06 - 3.36e-03 7.69e-02f 1 44r 1.7598365e+03 4.50e+06 8.17e+03 -5.7 2.24e+06 - 4.43e-08 4.23e-02f 1 45r 5.7264420e+03 2.36e+06 4.60e+03 -5.7 2.14e+06 - 7.07e-02 1.00e+00f 1 46 4.3546591e+03 2.35e+06 1.50e+01 -1.0 2.51e+08 - 3.52e-03 2.97e-03f 1 47 3.7700543e+03 2.16e+06 1.94e+01 -1.0 2.87e+06 - 3.27e-01 8.10e-02f 1 48 3.9963720e+03 1.02e+06 7.97e+00 -1.0 3.70e+05 - 3.47e-01 5.26e-01h 1 49 4.0601733e+03 5.28e+05 5.09e+00 -1.0 1.57e+06 - 5.24e-03 4.85e-01h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls 50 4.0596593e+03 5.27e+05 3.53e+00 -1.0 4.32e+06 - 7.60e-01 1.81e-03h 1 51 4.1577305e+03 9.40e+04 7.32e-01 -1.0 4.01e+05 - 9.09e-01 8.22e-01h 1 52 4.1754490e+03 1.27e+01 4.74e-02 -1.0 5.08e+04 - 8.32e-01 1.00e+00h 1 53 4.1752565e+03 7.78e-02 8.68e-07 -1.0 1.49e+04 - 1.00e+00 1.00e+00h 1 54 4.1704409e+03 1.60e+00 3.18e-05 -2.5 1.16e+04 - 1.00e+00 1.00e+00f 1 55 4.1704236e+03 6.98e-04 2.83e-08 -2.5 1.41e+03 - 1.00e+00 1.00e+00h 1 56 4.1702897e+03 1.15e-03 2.31e-08 -3.8 2.98e+02 - 1.00e+00 1.00e+00f 1 57 4.1702823e+03 3.63e-06 5.75e-11 -5.7 1.67e+01 - 1.00e+00 1.00e+00h 1 58 4.1702822e+03 1.28e-09 1.62e-14 -8.6 2.04e-01 - 1.00e+00 1.00e+00h 1 Number of Iterations....: 58 (scaled) (unscaled)
Objective...............: 4.1702822027548118e+03 4.1702822027548118e+03
Dual infeasibility......: 1.6235231869939369e-14 1.6235231869939369e-14
Constraint violation....: 1.2805685400962830e-09 1.2805685400962830e-09
Complementarity.........: 2.5079038009909822e-09 2.5079038009909822e-09
Overall NLP error.......: 2.5079038009909822e-09 2.5079038009909822e-09 Number of objective function evaluations = 63
Number of objective gradient evaluations = 16
Number of equality constraint evaluations = 63
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 60
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 58
Total CPU secs in IPOPT (w/o function evaluations) = 0.682
Total CPU secs in NLP function evaluations = 0.002 EXIT: Optimal Solution Found.

Summary

We used various examples, front ends, and solvers to solve numerical optimization problems using SageMaker Processing. Next, try using Scipy.optimize, DEAP, or Inspyred to explore other examples. See the references in the next section for documentation and other examples to help solve your own business problems using SageMaker Processing. If you currently use SageMaker APIs for your machine learning projects, using SageMaker Processing for running optimization is a simple, obvious extension. However, consider that other compute options on AWS such as Lambda or Fargate may be more relevant when running some of these open source libraries for serverless optimization, especially when your team has this expertise. Lastly, open source libraries are provided as is, with minimal support whereas commercial libraries such as CPLEX and Gurobi are constantly being tuned for higher performance, and usually provide premium support.

References

About the Author

Shreyas SubramanianShreyas Subramanian is a AI/ML specialist Solutions Architect, and helps customers by using Machine Learning to solve their business challenges using the AWS platform.

Posted inAWS News
TagsAWS